GIS 데이터를 다루다 보면 이 두 단어는 상당히 많이 보실 겁니다.
특히 제일 머리 아플 때는 이미지 좌표계와 공간 좌표계 간 원점 위치의 차이일 겁니다. 오늘은 이 헷갈리는 점을 짚고 넘어가려 합니다.
개요
포스팅의 목적
- gdal의 geotransform의 개념과 구성 요소를 알아보자
- gdal에서는 어던 좌표계 체계를 채택하고 있는지 알아보자
- 이미지를 georeference하려면 어떻게 해야할까? 이미지 좌표계와 공간 좌표계 간의 차이에 주의하자.
개념
이미지 좌표계? 공간 좌표계?
이미지 좌표계

위 그림은 우리가 알고리즘 문제를 풀 때 많이 접하는 배열의 형태입니다. 가로(width)를 column, 세로(height)를 row로 대응합니다.원점은 좌상단부터 시작합니다.
이미지 좌표계에서도 위와 같은 형태로 배열을 취급합니다.
공간 좌표계

왼쪽 그림에 나와 있듯 공간 좌표계는 우리가 수학에서 접했던 x,y 평면을 생각하시면 쉽습니다. x축에는 latitude(위도), y축에는 longitude(경도)를 대응합니다.원점은 좌하단부터 시작합니다.
경위도라고 말할 때도 있고, 위경도라고 얘기할 때도 있는데 영어로 얘기하다가 이렇게 한글에서 순서를 바꾼 단어를 만나면 저도 헷갈립니다.
x-y 순서로 취급하면 위경도라고 말하는게 덜 헷갈리겠네요.
오른쪽 그림은 이미지 좌표의 형태를 다시 한번 더 언급합니다.
GIS에서 자주 다루는 gdal 라이브러리에서는 어떤 방법을 사용할까요?
GDAL의 좌표계 개념
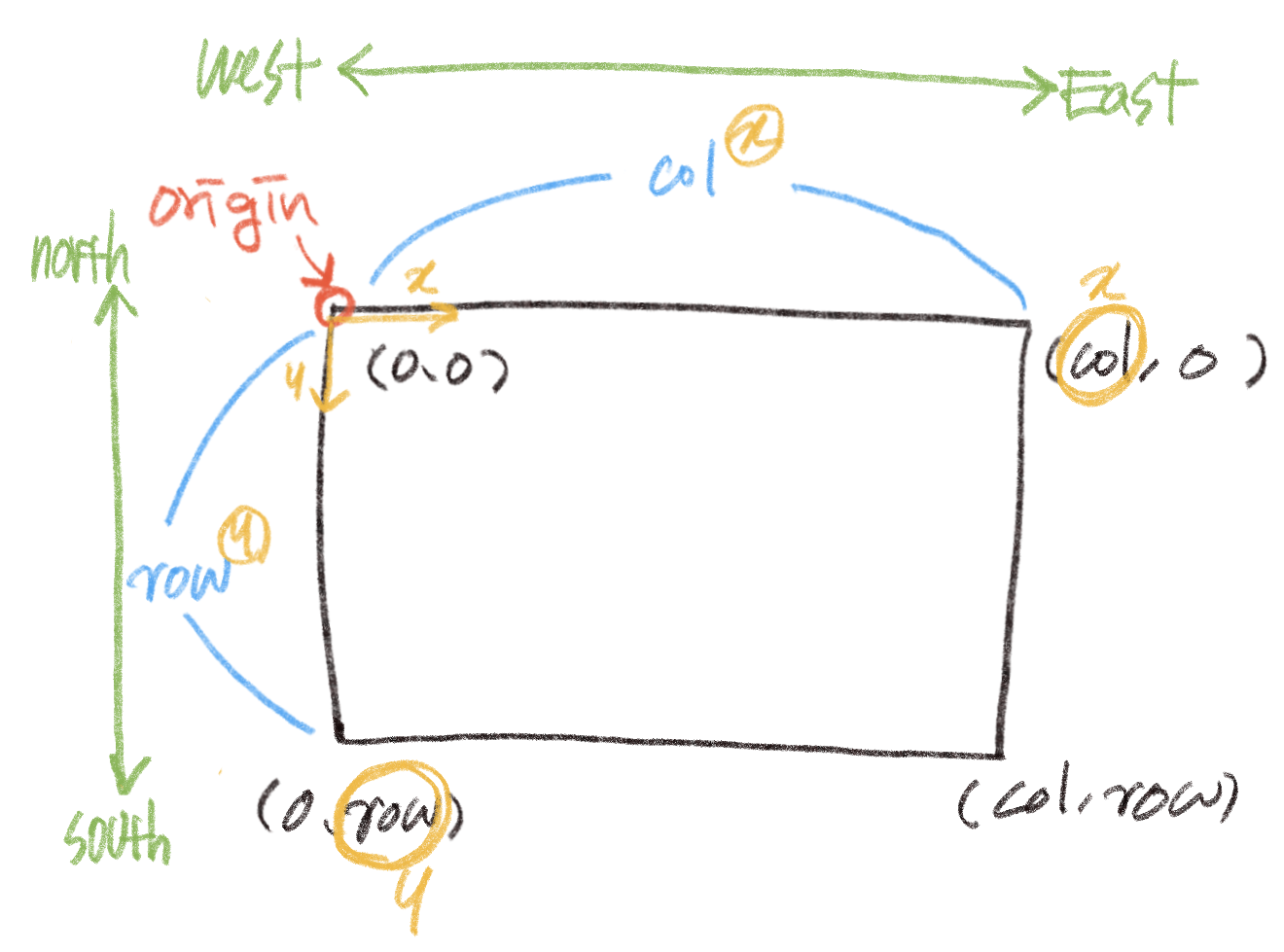
제가 직접 그린 그림으로 설명을 하겠습니다.
먼저 gdal의 좌표계는 좌상단이 origin입니다.x를 col, y를 row에 매칭합니다. x,y라고 불러야 할 때 col, row 순으로 부릅니다. 따라서 좌하단의 좌표는 (0,row), 우상단의 좌표는 (col,0)이 됩니다. GCP(Ground Control Point)를 설정할 때 순서는 좌상단 -> 좌하단 -> 우하단 -> 우상단으로 시계 반대 방향을 지켜주시면 됩니다.
geotranfrom
해당 개념에 대한 자세한 내용은 공식문서를 참고하세요. geotransform의 원리는 다음과 같습니다. 이미지 좌표계로 표현된 데이터를 실세계에 전개하기 위해 공간 좌표계로 투영을 변환합니다. 이 때, 선형 변환의 종류 중 하나인 affine transformation을 거칩니다.(선형대수학을 참고하세요)
gdal에서는 affine transformation을 지원하기 위한 파라미터를 아래와 같이 정의하고 있습니다.
GT(0) x-coordinate of the upper-left corner of the upper-left pixel.
GT(1) w-e pixel resolution / pixel width.
GT(2) row rotation (typically zero).
GT(3) y-coordinate of the upper-left corner of the upper-left pixel.
GT(4) column rotation (typically zero).
GT(5) n-s pixel resolution / pixel height (negative value for a north-up image).- 0번째 : 좌상단 점(origin)의 x 좌표
- 1번째 : 횡방향의 픽셀 해상도(resolution) ⇒ 픽셀 하나의 가로 크기가 실제 좌표계 내의 길이와 어떻게 매칭되는가?
- 2번째 : x축 방향으로의 회전
- 3번째 : origin의 y좌표
- 4번째 : y축 방향으로의 회전
- 5번째 : 종방향의 픽셀 해상도(resolution) ⇒ 픽셀 하나의 세로 크기가 실제 좌표계 내의 길이와 어떻게 매칭되는가?
- 단위 : 좌표계의 단위를 따라감. EPSG:4326에서는 degree, EPSG:3857에서는 m
GeoReference
이 개념은 이미지에 위치 정보를 적용해 지도 위에 이미지 데이터를 시각화할 수 있는 상태로 만든다는 의미입니다.GIS 라이브러리를 이용해 geotiff를 다루려면 반드시 알아야 하는 개념입니다.
위에서 설명한 GeoTransform을 사용해 GeoReference를 적용하는 코드를 서술하겠습니다.
해당 코드에서는 좌상단, 우하단 두 점을 직사각형을 가로지르는 기준선으로 사용합니다. 이 직사각형은 이미지의 extent가 됩니다.
좀 더 복잡한 수준의 GeoReference는 다음 포스팅에서 언급하겠습니다.
'''
raster_path : 데이터를 저장할 경로
raster_arr : 이미지 데이터를 numpy.array로 저장한 형태
band_num : raster_arr의 차원수
epsg_code : 공간 좌표계의 epsg 코드명. 숫자로 기입합니다.
upper_left_lonlat : (경도, 위도)순으로 이미지가 투영될 장소(직사각형이라 가정합니다)의 좌상단 좌표를 기입합니다.
lower_right_lonlat : (경도, 위도)순으로 이미지가 투영될 장소의 우하단 좌표를 기입합니다.
'''
def make_georeference(raster_path, raster_arr, band_num, epsg_code, upper_left_lonlat, lower_right_lonlat) :
format = "GTiff"
driver = gdal.GetDriverByName( format )
metadata = driver.GetMetadata()
# 가로세로 정보 가져오기
col = raster_array.shape[0]
row = raster_array.shape[1]
# 좌하단, 우하단 좌표 만들기
upper_right_lonlat = (lower_right_lonlat[0],upper_left_lonlat[1])
lower_left_lonlat = (upper_left_lonlat[0],lower_right_lonlat[1])
# 좌상단 -> 좌하단 -> 우하단 -> 우상단
gcp_list = [(*(0,0),*(upper_left_lonlat)),(*(0,row),*(lower_left_lonlat)),\
(*(col,row),*(lower_right_lonlat)),(*(col,0),*(upper_right_lonlat))]
# 좌상단, 좌하단, 우하단, 우상단 점을 가지고 gcp(ground countrol point)를 만드는 코드
gdal_gcp_list = []
for item in gcp_list:
pixel, line, x, y = map(float, item)
z = 0
gcp = gdal.GCP(x, y, z, pixel, line)
gdal_gcp_list.append(gcp)
dst_ds = None
# single channel일 때
if band_num == 1 :
dst_ds=driver.Create(raster_path, col, row, 1 ,gdal.GDT_Float32,options = [ 'PHOTOMETRIC=MINISBLACK' ])
dst_ds.GetRasterBand(1).WriteArray(raster_arr)
# RGB channel일 때
else :
dst_ds=driver.Create(raster_path, col, row, band_num ,gdal.GDT_Float32,options = [ 'PHOTOMETRIC=RGB' ])
for i in range(1, band_num+1) :
dst_ds.GetRasterBand(i).WriteArray(raster_arr[:,:,i-1])
proj = osr.SpatialReference()
proj.ImportFromEPSG(int(epsg_code))
dst_ds.SetProjection(proj.ExportToWkt())
# gcp로부터 geotransform을 계산
geotransform = gdal.GCPsToGeoTransform(gdal_gcp_list)
'''
대부분의 라이브러리는 이 geotransform을 읽어 geotiff를 제어한다.
gcp만 세팅하는 경우 대부분 읽어들이지 못한다.
gcp만 세팅하는 경우는 다른 문서에서 다루도록 한다.
'''
dst_ds.SetGeoTransform(list(geotransform))
dst_ds = None코드 설명입니다.
# 좌하단, 우하단 좌표 만들기
upper_right_lonlat = (lower_right_lonlat[0],upper_left_lonlat[1])
lower_left_lonlat = (upper_left_lonlat[0],lower_right_lonlat[1])
# 좌상단 -> 좌하단 -> 우하단 -> 우상단
gcp_list = [(*(0,0),*(upper_left_lonlat)),(*(0,row),*(lower_left_lonlat)),\
(*(col,row),*(lower_right_lonlat)),(*(col,0),*(upper_right_lonlat))]우리는 좌상단 좌표와 우하단 좌표를 알고 있습니다. 이 말은 경위도의 min,max값을 알고 있다는 말과 동일합니다.
이를 통해 직사각형의 나머지 두 꼭지점을 구할 수 있습니다. 이렇게 직사각형의 네 꼭지점을 만들고 이를 GCP로 만듦니다.
proj = osr.SpatialReference()
proj.ImportFromEPSG(int(epsg_code))
dst_ds.SetProjection(proj.ExportToWkt())
# gcp로부터 geotransform을 계산
geotransform = gdal.GCPsToGeoTransform(gdal_gcp_list)
...
dst_ds.SetGeoTransform(list(geotransform))직사각형을 만들 수 있다면 하나의 평면을 만들 수 있다는 말과 같습니다. 이 평면을 하나의 공간 좌표계로 취급하면,
기존의 이미지 좌표계에서 이 공간 좌표계로 affine transformation을 적용해 변환이 필요합니다. 즉, geotransformaion의 계산이 필요합니다.
gdal은 gdal.GCPsToGeoTransform이라는 함수를 제공합니다. 우리가 앞에서 구한 GCP로 geotransform을 구할 수 있습니다.
다만 이 함수를 통해 얻은 geotransformaion을 SetGeoTransform으로 이미지 정보에 반영하게 되면 기존에 설정한 GCP는 사라지게 되니 주의하세요.
결론
이번 포스팅에서는 이미지 좌표계와 gis 좌표계 간의 차이점을 알아봤습니다. 그리고 numpy.array형태의 이미지 데이터에 어떻게 위치 정보를 입혀서 geotiff로 저장하는지 간단한 코드를 통해 알아봤습니다.
레퍼런스
- 이미지 좌표계와 공간 좌표계 간 차이 : https://mirametrics.com/help/mira_pro_script_8/source/pixel_coordinate_definition.htm
- affine transformation : https://www.perrygeo.com/python-affine-transforms.html
'GIS' 카테고리의 다른 글
| [GeoPandas] 사용 시 알아두면 좋은 점들 (0) | 2024.08.05 |
|---|---|
| [GeoTIFF] GEOS projection을 따르는 위성 영상을 EPSG:4326으로 재투영하는 방법 (2) | 2024.08.04 |
| Matplotlib Basemap Toolkit으로 tiff 데이터 시각화하기 (기초) (0) | 2024.05.14 |
| [GIS] gcp로 georeference 하기, lcc 좌표계에서 EPSG:4326으로 reproject 하기 (3) | 2023.02.28 |
| [ArcGIS] ArcGIS python API 기초 예제 (2) | 2023.01.31 |
