GIS 엔지니어로 수많은 좌표계를 다루지만, 보통은 Mercator projection이 기반인 좌표계를 주로 다룹니다.
그런데 말입니다,
어느날 혜성과도 같이 이 GEOS projection이라는 녀석이 절 찾아왔습니다.
악몽의 시작이었죠.
1년은 시달린 것 같습니다.
얘는 이전에 썼던 글인 GeoTransform과 GeoReference에서
georeference를 처리하는 방법에 추가로 필요한 요소가 있습니다.
그리고 얼마 전에 제가 드디어 방법을 찾았습니다.
오늘 글의 숨은 주제는 정답이 없는 문제를 푸는 과정이기도 합니다.
- 작은 실마리 찾기
- 다른 사례를 보면서 역엔지니어링하기
- 메뉴얼이 부족한 경우 배경 지식을 활용해서 값들을 계산해서 구하기
- 역엔지니어링한 경우와 내 해결방법을 교차 검증하기
개요
포스팅의 목적
- GEOS projection은 무엇인가?
- GEOS projection을 따르는 위성 영상은 어떻게 처리해야 하는가?
- GEOS projection을 따르는 위성 영상을 어떻게 EPSG:4326을 따르는 geotiff로 만들 것인가?
개념
GEOS projection
이전에 다뤘던 projection은 Mercator projection이라고 앞에서 언급했죠.

위 사진과 같이 원통 안에 지구를 넣고, 지구 중심에서 빛을 쏜다고 가정했을 때 이 빛이 원통에 지구를 어떻게 비추는지를 계산해서 지구를 2차원 평면에 나타내는 투영법 중 하나가 Mercator projection입니다.
하지만 GEOS projection은 시작점부터가 다릅니다.
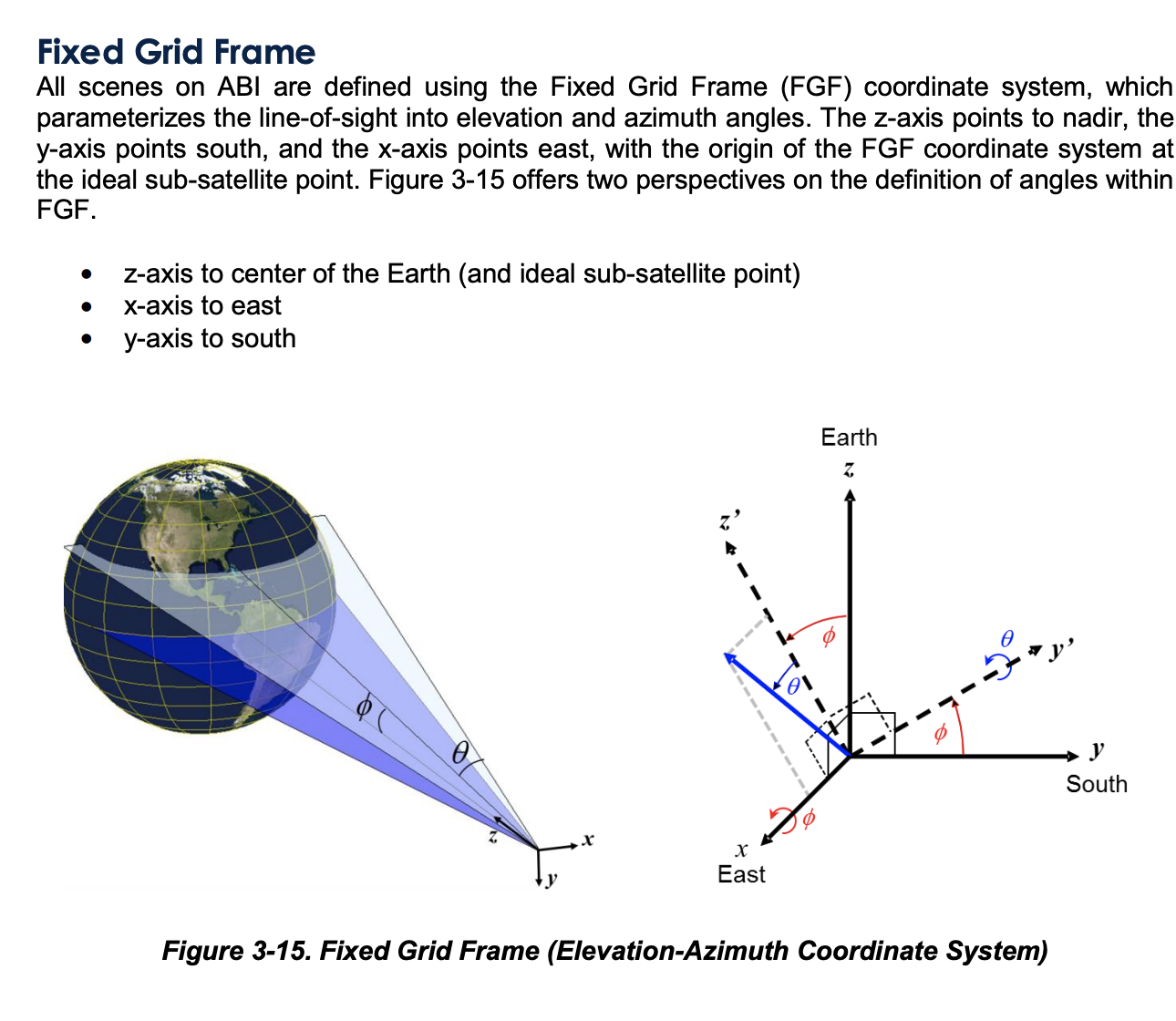
미국 위성 중 하나인 GOES 시리즈에서 자신들이 어떤 투영법을 쓰고 있는지 그 원리를 설명하는 그림 중 일부분을 발췌해왔습니다.
출처
시작 시점이 지구 중심이 아닙니다. 지구 바깥쪽에서 위성이 지구를 바라볼 때를 생각한 투영법이 바로 GEOS projection입니다.
이렇다 보니, 이를 2차원으로 옮기기 위해 기존 Mercator projection과는 다르게 Proj의 설정값을 다르게 해줘야 합니다.
Proj
Proj는 Coornidate Reference System(CRS, 우리는 이를 한국어로 좌표계라고 많이들 얘기합니다) 간의 변환을 지원하기 위해 각 좌표계를 정의하는 변수를 정의합니다.
하지만...! GEOS projection는 투영법 방법이지 실제 다루는 위성 영상에 따라 세세한 변수 값이 바뀝니다.
오늘 할 얘기는 이 세세한 변수 값들을 찾아가는 과정입니다.
Proj 변수 계산하기
역엔지니어링 - GOES 16 시리즈 (+ 작은 실마리 찾기 1)
미국의 GOES-16 시리즈 위성 영상은 netCDF 파일로 제공됩니다. 그리고 놀라운 사실 하나.
gdal_translate -ot float32 -unscale -CO COMPRESS=deflate NETCDF:"OR_ABI-L1b-RadF-M3C02_G16_s20171921545382_e20171921556149_c20171921556183.nc":Rad fulldisk.tif이렇게 GOES-16 데이터에는 별도 옵션 설정 없이 바로 geotiff로 변환할 수 있었습니다.
그래서 GOES-16 데이터를 geotiff로 변환한 파일을 분석했습니다. 그 중에서 주목할 부분들을 발췌해왔습니다.
역엔지니어링2 - GOES 16 시리즈 분석 코드 (+ 작은 실마리 찾기 2)
GOES는 그 위상 답게 데이터를 다루는 라이브러리도 존재합니다.
GOES 위성을 다루는 python 코드를 찾으면서 goes2go라는 라이브러리를 알게 되었습니다. 여기 코드 중에 아래 코드에서 작은 힌트를 얻게 됩니다.
p = ABI["goes_imager_projection"]
# The projection x and y coordinates equals the scanning angle (in radians)
# multiplied by the satellite height See details here:
# https://proj4.org/operations/projections/geos.html?highlight=geostationary
'''
아래 코드에서 GroundControlPoint(GCP)가 직접 측정한 값이 아닌 계산된 값임을 알았습니다. 그리고 원래 radian으로 제공되는데
여기에 지표면과 위성 간의 거리 값을 곱해 GEOS projection 내의 좌표값을 제공함을 알았습니다.
'''
x = ABI["x"][:] * p.perspective_point_height
y = ABI["y"][:] * p.perspective_point_height
######################################################################
# The geostationary projection is the easiest way to plot the image on a
# map. Essentially, we are stretching the image across a map with the same
# projection and dimensions as the data.
try:
print("first try...", end="")
globe = ccrs.Globe(
semimajor_axis=p.semi_major_axis,
semiminor_axis=p.semi_minor_axis,
inverse_flattening=p.inverse_flattening,
)
geos = ccrs.Geostationary(
central_longitude=p.longitude_of_projection_origin,
satellite_height=p.perspective_point_height,
sweep_axis=p.sweep_angle_axis,
globe=globe,
)
except:
print("second try")
globe = ccrs.Globe(
semimajor_axis=p.semi_major_axis[0],
semiminor_axis=p.semi_minor_axis[0],
inverse_flattening=p.inverse_flattening[0],
)
geos = ccrs.Geostationary(
central_longitude=p.longitude_of_projection_origin[0],
satellite_height=p.perspective_point_height[0],
sweep_axis=p.sweep_angle_axis,
globe=globe,
)첫 번째 실마리입니다.
x = ABI["x"][:] * p.perspective_point_height
y = ABI["y"][:] * p.perspective_point_height위 코드에서 GroundControlPoint(GCP)가 직접 측정한 값이 아닌 계산된 값임을 알았습니다. 그리고 원래 radian으로 제공되는데
여기에 지표면과 위성 간의 거리 값을 곱해 GEOS projection 내의 좌표값을 제공함을 알았습니다.
두 번째 실마리입니다.
try:
print("first try...", end="")
globe = ccrs.Globe(
semimajor_axis=p.semi_major_axis,
semiminor_axis=p.semi_minor_axis,
inverse_flattening=p.inverse_flattening,
)
geos = ccrs.Geostationary(
central_longitude=p.longitude_of_projection_origin,
satellite_height=p.perspective_point_height,
sweep_axis=p.sweep_angle_axis,
globe=globe,
)위 코드에서는 구를 정의하는 값들을 알 수 있습니다. ccrs.Globe에는 지구를 수학적으로 정의하는 타원체의 구성 값들을 서술하고 있습니다.
ccrs.Geostationary에서는 GEOS projection을 정의하는 데 필요한 값들을 알 수 있었습니다.
대략적으로 필요한 값들을 찾았군요.
semi_major_axis
semi_minor_axis
inverse_flattening
central_longitude
satellite_height
sweep_axis
globe이 값들이 어떤 의미를 가지고, 어떻게 활용되는지는 아래 파트에서 상술하겠습니다.
geotiff 분석하기
REMARK["PROJ CRS string: +proj=geos +lon_0=-75 +h=35786023 +x_0=0 +y_0=0 +ellps=GRS80 +units=m +no_defs +sweep=x"]]
Origin = (-5434894.700982173904777,5434894.700982173904777)
Upper Left (-5434894.701, 5434894.701)
Lower Left (-5434894.701,-5434895.218)
Upper Right ( 5434895.218, 5434894.701)
Lower Right ( 5434895.218,-5434895.218)
Center ( 0.2586200, -0.2586200) ( 74d59'59.99"W, 0d 0' 0.01"S)여기서 우리가 파악할 수 있는 사항들은 다음과 같습니다.
- Proj 변수 값
"PROJ CRS string: +proj=geos +lon_0=-75 +h=35786023 +x_0=0 +y_0=0 +ellps=GRS80 +units=m +no_defs +sweep=x"
- proj=geos : projection 방법
- lon_0 : 중심이 되는 longitude의 정보
- h : 지구 표면 부터 위성 까지의 높이
- ellps=GRS80 : 구를 수학적으로 정의한 방법들 중 GRS80을 채택
- Upper Left ~ Lower Right : GEOS Projection에서 정의된 위성 영상의 네 귀퉁이의 위치입니다.
- Center : Radian 값입니다. 1번의 lon_0값을 radian으로 바꾸면 이렇게 되기도 한데요, 자세한 내용은 후에 서술하겠습니다.
netCDF 분석하기
그렇다면 이 값들을 netCDF에서 어떻게 구할 수 있을까요?
netCDF의 변수들을 조회한 결과는 다음과 같습니다.
long_name: GOES-R ABI fixed grid projection
grid_mapping_name: geostationary
perspective_point_height: 35786023.0
semi_major_axis: 6378137.0
semi_minor_axis: 6356752.31414
inverse_flattening: 298.2572221
latitude_of_projection_origin: 0.0
longitude_of_projection_origin: -75.0
sweep_angle_axis: x필요한 변수는 다음과 같습니다.
grid_mapping_name : projection (GEOS를 풀어쓰면 geostationary입니다.)
perspective_point_height : 지표면 ~ 위성 간의 거리
semi_major_axis : 지구는 sphere로 수학적으로 정의되는데, 축을 2개 씁니다. 그 중 장축의 값입니다.
semi_minor_axis : 위의 변수는 장축, 이 변수는 단축의 값입니다.
longitude_of_projection_origin : 정지 궤도에서 촬영하므로, 위성의 위치를 나타냅니다. 적도를 지나가는 정지 궤도 입니다.GK2A에 적용하기
netCDF 분석하기
이 포스팅에는 GK2A의 FullDisk 데이터를 매핑하는 GEOS Projection을 정의하는 변수를 찾기 위한 머나먼 여정 끝에 얻은 답이 담겨있습니다.
GK2A에서 제공하는 netCDF 파일을 분석하니 다음과 같습니다.
satellite_name: GK-2A
instrument_name: AMI
projection_type: GEOS
nominal_satellite_height: 42164000.0
earth_equatorial_radius: 6378137.0
earth_polar_radius: 6356752.3
image_center_latitude: 0.0
image_center_longitude: 2.2375121010567307
image_upperleft_x: -0.153972
image_upperleft_y: 0.153972
image_lowerright_x: 0.153972
image_lowerright_y: -0.153972- nominal_satellite_height : 지구 중심 ~ 위성까지의 거리입니다.
- earth_equatorial_radius : 지구를 수학적으로 정의하는 sphere의 장축입니다.
- earth_polar_radius : 단축입니다.
- image_center_longitude : 원래는 128.2도인데 이걸 radian으로 바꾼 값입니다.
- image_upperleft_x ~ image_lowerright_y : 이 값들의 단위를 모르겠지만, 다음의 식에 의해 값을 radian으로 바꿀 수 있습니다.이 계산식을 각각의 값에 적용하면 다음과 같은 값을 얻을 수 있습니다.
Upper Left (-5434894.701, 5434894.701)
Lower Left (-5434894.701,-5434895.218)
Upper Right ( 5434895.218, 5434894.701)
Lower Right ( 5434895.218,-5434895.218)
#{image_upperleft_x} * {nominal_satellite_height - semi_major_axis} = {image_upperleft_x in radian}Proj
GOES에서 얻었던 값을 살짝 변형해봅시다.
기상청에서 얻을 수 있는 GK2A 데이터 좌표계 설명 메뉴얼에는 GK2A의 GEOS projection은 WGS84를 구로 쓴다고 합니다
"PROJ CRS string: +proj=geos +lon_0=-128.2 +h=35786023 +x_0=0 +y_0=0 +ellps=WGS84 +units=m +no_defs +sweep=x"변환 코드
from osgeo import gdal
from osgeo import osr
import numpy as np
from netCDF4 import Dataset
'''
이 함수는 이미지의 경계점을 적합한 값으로 변환하고, GDAL의 GCP 객체로 변환하는 함수입니다.
'''
def gk2a_get_corner_gcps() :
# image_bound_value = (nominal_satellite_height - semi_major_axis) * image_upperleft_y
image_bound_value = 5510020.897836
upper_left = (-image_bound_value, image_bound_value)
lower_left = (-image_bound_value, -image_bound_value)
upper_right = (image_bound_value, image_bound_value)
lower_right = (image_bound_value, -image_bound_value)
upper_left_gcp = (upper_left[0], upper_left[1], 0, 0, 0)
lower_left_gcp = (lower_left[0], lower_left[1], 0, 5500, 0)
upper_right_gcp = (upper_right[0], upper_right[1], 0, 0, 5500)
lower_right_gcp = (lower_right[0], lower_right[1], 0, 5500, 5500)
gcp_list = [upper_left_gcp, lower_left_gcp, upper_right_gcp, lower_right_gcp]
gdal_gcp_tuple_list = []
for gcp in gcp_list :
x,y,z,pixel,line = gcp
gdal_gcp_tuple_list.append(gdal.GCP(x,y,z,pixel, line))
return gdal_gcp_tuple_list
'''
아래 함수는 gk2a의 2km 해상도 데이터를 지원합니다.
1.0km, 0.5km 해상도도 변수가 크게 달라지지 않아서 이 함수로 대응 가능할 듯 합니다.
hasnodata는 nodata value를 설정할 거냐고 묻는 플래그입니다.
gk2a의 데이터는 경우마다 다르겠지만 IR 채널(10.5)은 32768을 nodata로 쓰고 있습니다.
'''
def gk2a_nc_to_tiff(nc_path, geotiff_path, hasnodata=True) :
width = 5500
height = 5500
proj_wkt_str = "+proj=geos +lon_0=128.2 +h=35786023 +x_0=0 +y_0=0 +ellps=WGS84 +units=m +no_defs +sweep=x"
gdal_gcp_list = gk2a_get_corner_gcps()
out_srs = osr.SpatialReference()
out_srs.ImportFromProj4(proj_wkt_str)
nodata_value = 32768
data_type = gdal.GDT_Float32
band_num = 1
photometric_type = 'PHOTOMETRIC=MINISBLACK'
# geotiff 생성 기본 변수들
driver = gdal.GetDriverByName("GTiff")
dst_ds = driver.Create(geotiff_path, width, height, band_num, data_type,options=[photometric_type])
# 이미지의 상하좌우 구석의 점을 GCP로 설정하면서 이미지의 extent를 지정하는 효과를 볼 수 있습니다.
dst_ds.SetGCPs(gdal_gcp_tuple_list, out_srs.ExportToWkt())
dst_ds.SetProjection(out_srs.ExportToWkt())
gk2a_nc = Dataset(nc_path)
gk2a_arr = gk2a_nc["image_pixel_values"][:]
dst_ds.GetRasterBand(1).WriteArray(np.transpose(gk2a_arr))
if hasnodata :
dst_ds.GetRasterBand(1).SetNoDataValue(nodata_value)
# 웹에 데이터를 표출하기 위해서 GeoTransform값이 반드시 필요합니다.
dst_ds.SetGeoTransform(gdal.GCPsToGeoTransform(gdal_gcp_tuple_list))
dst_ds = None
def geos_to_4326(prev_geotiff_path, new_geotiff_path) :
input_ds = gdal.Open(prev_geotiff_path)
output_ds = gdal.Open(new_geotiff_path)
warp = gdal.Warp(output_ds, input_ds, dstSRS='EPSG:4326')
warp = None
output_ds = None
input_ds = None이 함수들을 모두 적용했을 때의 예시 결과물은 다음과 같습니다.
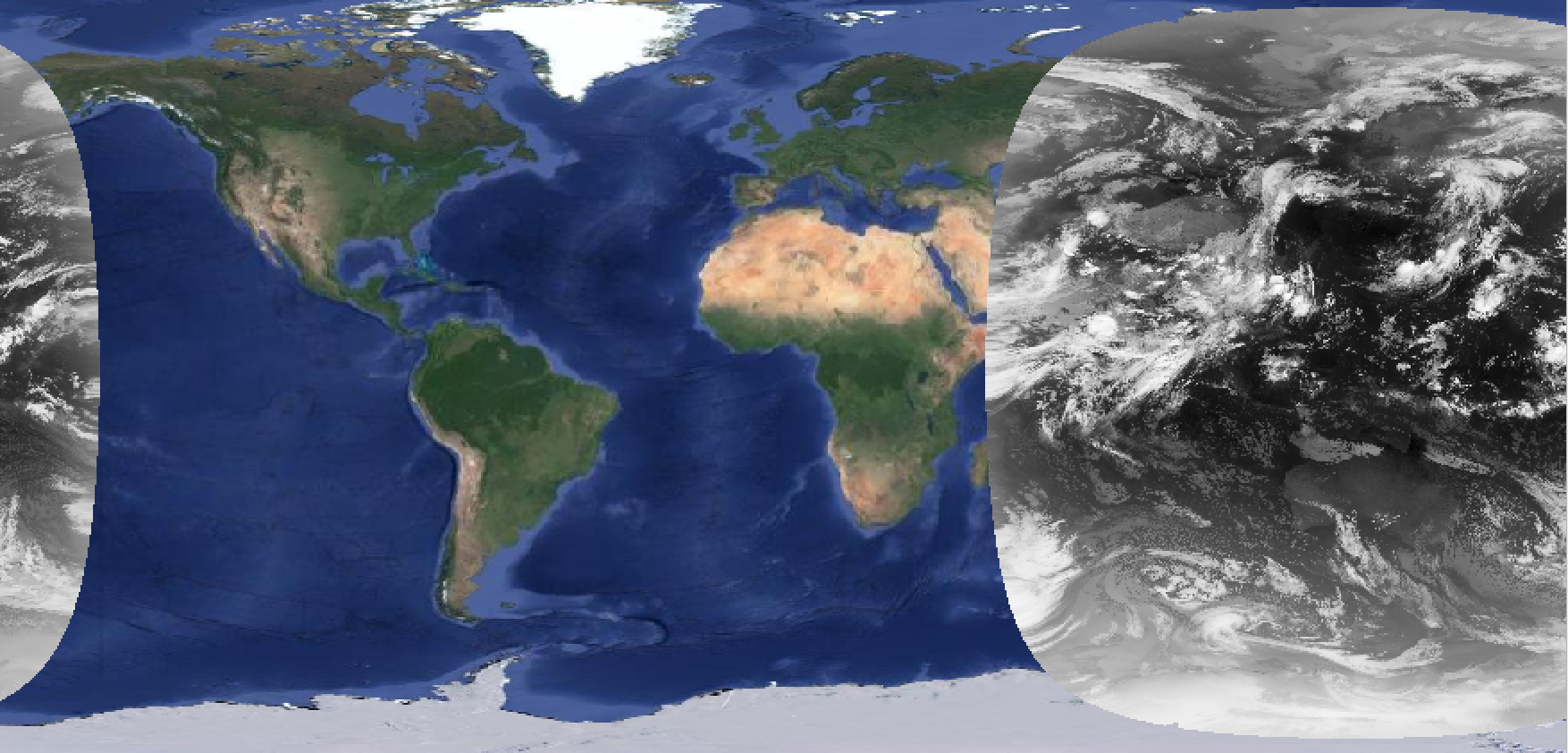
결론
이 방법을 찾기까지 부담이 컸습니다. NASA라던가 EUMETVIEW에서는 GEOS projection을 따르는 데이터를 예쁘게 표출하는데, 나는 왜 못하는가...!
많이 답답했는데 이렇게 제가 문제를 해결한 한 사례를 여러분들과 공유할 수 있어서 기쁩니다.
이 포스팅은 공익을 위해 작성했습니다. GK2A 메뉴얼이 존재하긴 한데 좀 빠진 부분이 있어서 제가 값을 스스로 계산하면서 검증한 부분들도 있습니다.
이 포스팅에서는 얻은 결과 위주로 간결하게 작성했습니다. GK2A FullDisk 데이터로 헤매이는 여러분들에게 좋은 결과가 있길 바라면서...!
참고문헌
Proj GEOS 변수
GOES netCDF를 geotiff로
GOES에서 사용하는 GEOS projection 계산 원리
goes2go
GOES 데이터 AWS 다운로더
'GIS' 카테고리의 다른 글
| [GeoTIFF] GeoTIFF 파일의 corner coordinates를 구하자 (0) | 2024.10.30 |
|---|---|
| [GeoPandas] 사용 시 알아두면 좋은 점들 (0) | 2024.08.05 |
| GeoTransform과 GeoReference (0) | 2024.05.18 |
| Matplotlib Basemap Toolkit으로 tiff 데이터 시각화하기 (기초) (0) | 2024.05.14 |
| [GIS] gcp로 georeference 하기, lcc 좌표계에서 EPSG:4326으로 reproject 하기 (3) | 2023.02.28 |
